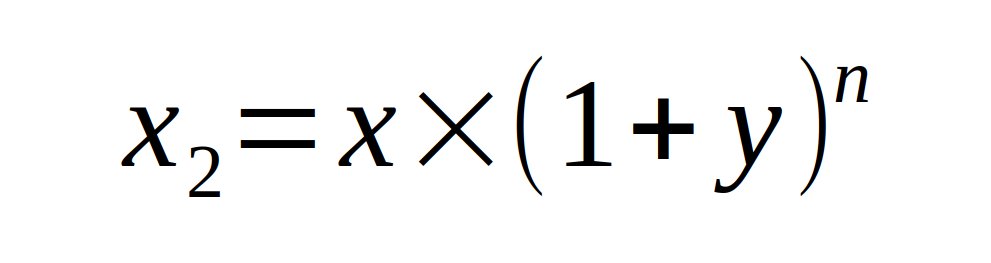Oh et si vous avez une source sur cette affaire de Theodor Mommsen ayant perdu ses cheveux dans l'incendie de sa bibliothèque, ça m'intéresse. Certains prétendent qu'il en est mort, ce dont je doute. @Nervia_Nocline c'est un peu ton domaine les classicistes allemands ?
@BrumeAdelaide et moi dans Valheim quand on va arriver dans la montagne.
Marche aussi pour Minecraft, dans une moindre mesure…
Ah, et j'ai vu l'affiche que vendredi (donc un poil tard, comme chaque année en fait), mais le festoche @filmerletravail c'est en ce moment jusqu'au 28 février, et dispo en ligne.
Un condensé des dernières vidéos d'@Heu7reka, en encore plus vulgarisé et accessible.
Quelqu'un pour nous expliquer pourquoi Les Trois Brigands paru aux Lutins de l'École des loisirs… est tiré de la version allemande dite « originale » de 1963, alors que l'auteur est français et a publié en anglais en 1961 ? J'suis sûr qu'il y a une histoire derrière.
Alors, grâce à @Arktos96 on a une explication complexe mais intéressante.
Tomi Ungerer était établi à New York. Il écrit et dessine les planches en 1960 et cherche à se faire éditer par Harper & Row (ou Harper & Brothers selon les sources). Mais l'éditrice n'aime pas. Elle veut changer la fin. Mécontent, Ungerer cherche un éditeur en Europe. C'est l'allemand Georg Lentz qui prend en charge, avec deux-trois nouvelles planches et un titre allemand. Ça, c'est en 1961. Sauf que la maison d'édition fait faillite en 1962. Je sais pas si Lentz a eu le temps de publier en propre ou si c'est resté dans les cartons. Pareil pour Harper & Row/Brothers.
En 1962, Ungerer réessaie en anglais avec les éditions américaines Atheneum Books qui publient sans la fin. Sauf que c'est pas fini pour la version originale allemande : la maison d'édition en faillite est rachetée par l'éditeur suisse Diogenes Verlag, qui publie en 1963 ce qu'on considère comme la première version allemande du texte. S'ensuit la traduction en français en 1968, sans doute en partie à cause des mésaventures d'édition de la version anglaise qu'a essuyé Ungerer, mais aussi parce qu'une maison d'édition suisse c'est à côté, ça parle aussi français, bref c'est simple.
Les sources : https://www.researchgate.net/publication/289693796_L'oeuvre_ouverte_de_Tomi_Ungerer_traductions_palimpsestes_et_transferts_interculturels (p. 103 sq.)
Ah mais je comprends mieux. Si @MarleneSchiappa n'a pas le temps de s'occuper de la situation des TDS, c'est parce que le droit des femmes à disposer de leur corps est non négociable mais s'applique seulement à la pilule -_-
Donc résumé de la conférence de presse de @VidalFrederique : on garde les concours, il y aura des plats à emporter pour les RU, et sinon démerdez-vous avec vos universités. J'veux dire, question bête : si vous vous reposez sur des cours et des examens à distance, comment feront les étudiants qui n'ont pas Internet/pas d'ordi/ont des gosses/aident les gens/postulent pour grossir les rangs des hôpitaux ? Vidal l'a dit tout à l'heure : on devra sur le long terme mettre en place bien plus d'enseignements à distance. Bon perso, j'ai entendu « … comme ça on pourra continuer de ne rien faire pour les universités » mais je pense être mentaliste sur les bords.
Voilà comment l'on fait, Monsieur @EmmanuelMacron. Je peux vous donner des cours si vous le souhaitez.
Notez qu'il ne me reste plus qu'une chômeuse (qui vient juste de sortir du lycée), et que dans l'ensemble mon chômage est resté en dessous du pourcent malgré les « conjonctures économiques »… Comme quoi…
Bon, eh bien après 10 mandats, mon plus grand échec aura été de ne pas atteindre les 80 % de satisfaction, avec 8 % de gosses « satisfaits » et non « heureux »…
« C'est une équation mathématique ! »
Alors @BasPhilippe il faudra nous expliquer ce qu'est une équation non mathématique et en quoi être mathématique prouve quoi que ce soit. Monsieur le sénateur, je vais vous montrer une équation mathématique.
Ceci est ce que j'ai retenu de mes années de lycée il y a plus de 10 ans. Vous étiez alors ministre des Affaires Sociales.
Cette équation devrait vous être familière. Elle permet de calculer un résultat de x après une croissance y maintenue pendant n années.
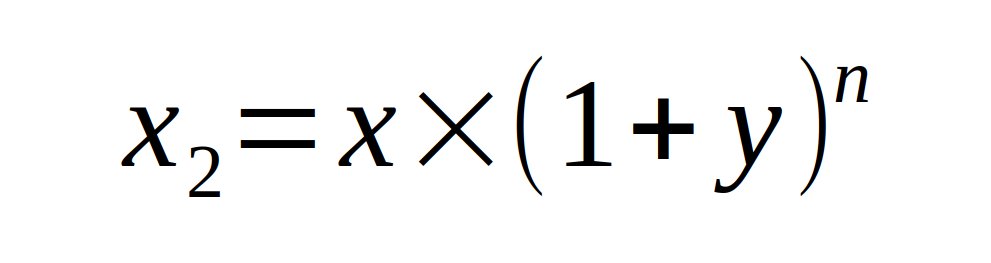
Passons à une démonstration mathématique.
Je m’appuierai sur le rapport de la DREES « Les retraités et les retraites » de 2018 portant sur les chiffres de 2016. Si vous en avez de plus récents, nous sommes tous preneurs. https://drees.solidarites-sante.gouv.fr/IMG/pdf/retraites_2018.pdf
Nous avons donc en 2016 :
Comme en France nous aimons nous projeter sur 30 ans, je vous propose de calculer la situation en 2050.
Comment le système des retraites devra faire face aux 34 × 200 000 = 6,8 millions nouveaux retraités ?
Comme la revalorisation des retraites se fait au petit bonheur la chance selon les besoins de trésorerie (gel en 2016, 0,1 % en 2015, 0,8 % en 2017), nous prendrons le taux fixé pour 2019 et 2020 de 0,3 %.
C'est là que notre équation entre en jeu. Alors, je n'ai plus les sources en tête, mais les prévisions de croissance jusqu'en 2050 étaient entre 1,6 et 1,7 % aux dernières nouvelles. Admettons un catastrophique 1,5 % sur toute la période. Reprenons notre équation pour calculer le PIB de 2050 :
2 228 × (1 + 0,015)^34 = 3 696 milliards d'euros
Il faudrait donc, en 2050 et par retraité :
19 130 × (1 + 0,003)^34 = 21 181 €
Le total pour 16,1 + 6,8 = 22,9 millions de retraités est donc de 21 181 × 22,9 = 485 milliards d'euros.
Cela paraît beaucoup, mais voici l'astuce : pendant ce temps, le PIB augmente aussi. Oh là là, les retraites pesaient 13,8 % au départ, elles pèsent 13,1 % à l'arrivée malgré les revalorisations et les quelques 7 millions de retraités supplémentaires ! Vite, il faut réformer, les retraites pèseront beaucoup trop sur notre économie dans 30 ans !
Nous avons donc en 2050 :
Mais vous savez aussi que depuis votre sortie de fonction les revalorisations sont en-deça de l'inflation. Autrement dit, admettre cela, c'est également admettre la baisse du niveau de vie des retraités orchestrée par l'État.
Voilà, Monsieur, je viens de vous démontrer mathématiquement qu'il n'y avait pas de problème de financement des retraites. Néanmoins vous pourriez m'adresser deux objections.
La première, c'est que la revalorisation des retraites est très en-deça de l'inflation. Il est vrai que depuis 2014 la revalorisation n'équivaut plus à celle de votre époque de ministre. Or, je vous rappelle le rapport de la DREES : le niveau de vie des retraités est supérieur à celui de l'ensemble de la population.
Admettre une baisse du niveau de vie des retraités, c'est donc admettre en même temps une baisse du niveau de vie général. Cela nous amène à votre seconde objection possible. La fameuse équation mathématique dont vous parlez serait celle du rapport cotisants/retraités. Le nombre de retraités augmentant, nous serions en passe d'arriver à une pénurie de cotisants, si je suis bien votre argumentation. Comme je viens de le démontrer mathématiquement, nous aurons besoin d'une fraction similaire des richesses produites pour subvenir aux besoins de l'augmentation des retraités.
Donc de deux choses l'une :
C'est un « ou bien » inclusif, bien entendu. Si nous manquons de cotisants, c'est donc que la part des richesses revenant aux cotisants n'est pas répartie correctement. Ce qui revient à dire, comme nous l'avons vu avec la première objection, que le niveau de vie de la population active est en baisse. Formuler ces deux objections revient ainsi à affirmer qu'une reforme dans la distribution des richesses est nécessaire puisque la distribution actuelle entraîne l'enrichissement d'un petit nombre qui ne profite pas au plus grand nombre. Je souhaite bien du courage à un quelconque Républicain osant avancer une telle proposition que d'aucun qualifierait de communiste voire d'extrême gauche.
Vous noterez, Monsieur @BasPhilippe que la force de mon argumentation mathématique repose entièrement sur la valeur que vous placez dans le terme « mathématique ». Admettriez-vous une valeur moindre, je suis disposé à débattre de ma démonstration.
J'adore ma directrice de mémoire. Par contre quand elle m'écrivait « je sais pas si le livre dont je vous donne la référence se trouve encore », j'avoue que je ne m'attendais pas à ce que la BU n'ait même pas une notice POUR L'AUTEUR DU BOUQUIN.
Bon, sur trois auteurs, on en a un seul référencé ici. Ça part mal. Si je dois compter sur Amazon, j'en ai pour 85 balles en trois bouquins, dont deux électroniques… Ça va être fun de regarder le prêt inter-universitaire patauger, quand je vois que même Bordeaux ne les a pas…
Victoire ! Il y en a un dispo en lecture en ligne à l'université de @Nervia_Nocline, j'ai plus qu'à lui faire les yeux doux \o/
