Affaire Macron-Benalla: les enregistrements qui changent tout : france
« C’était un film l’histoire quand même, hein ? […] On est entouré d'une bande de débiles […] »
J'avoue, Netflix peut aller se rhabiller…
franceinfo - Le nombre de créations d'entreprises a atteint un record en France en 2018
Ce n'est pas nouveau. Depuis 1987 (soit le moment où l'Insee a commencé à compter le nombre de créations d'entreprises) cela ne fait qu'augmenter. Certes, l'on a quelques années des baisses minimes, mais rien qui change durablement la tendance.
Ainsi, on peut titrer chaque année que c'est un record.
2017, un record. https://www.legifiscal.fr/actualites-fiscales/1770-creations-entreprises-7-2017.html https://www.economie.gouv.fr/entreprises/nombre-creation-entreprises-2017
2016, un record. https://www.economie.gouv.fr/entreprises/creation-entreprises-chiffres-2016
C'est même assez amusant d'aller faire une recherche sur l'Insee, les titres se ressemblent beaucoup.
Les créations d'entreprises poursuivent leur hausse en 2006 (Insee Première n° 1120) Un rythme des créations d'entreprises très élevé en 2007 (Insee Première n° 1172) La création d'entreprise en 2009 dopée par les auto-entrepreneurs (Insee Première n° 1277) Hors auto-entreprises, les créations d'entreprises augmentent en 2013 (Insee Première n° 1485)
Si vous allez voir les chiffres de l'Insee, la tendance reste stable depuis au moins 2008. Ça continue de grimper.
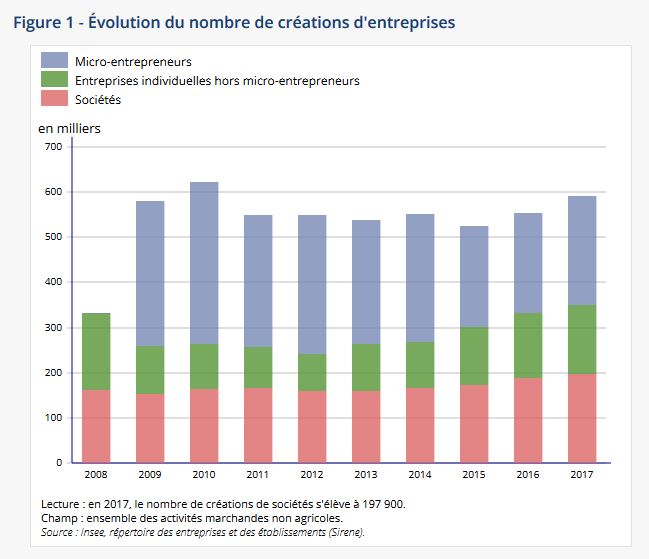
Si vous regardez les données dans leur ensemble, vous remarquez que cette tendance à grimper date à peu près du début des années 2000. Avant, c'est assez stable.
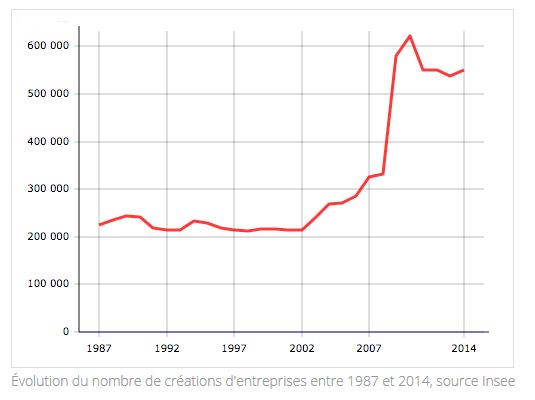
C'est également ce qu'on constate lorsque l'on regarde la part des non-salariés dans les emplois. Avant 2000 les non-salariés ont diminué, sans que ça n'engendre de création d'entreprise (données https://www.insee.fr/fr/statistiques/2424696).
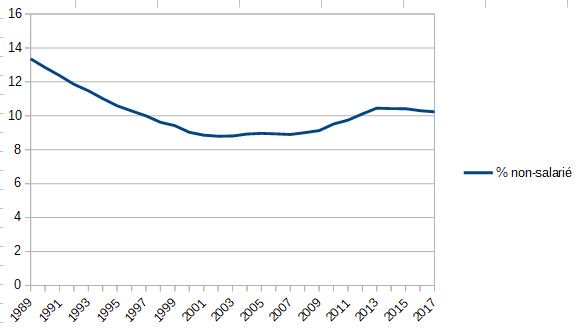
Maintenant si l'on reprend sur les dix dernières années ces mêmes données, là où tout le monde crie à un nouveau record, on voit que passé le boom de 2010-2013 avec les auto-entreprises, la part de non-salariés est stable, voire en baisse (mêmes données).
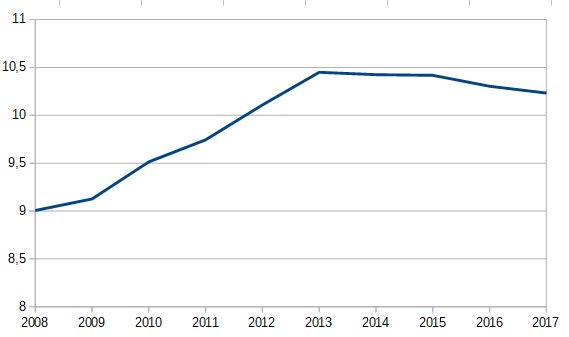
Parce que voyez-vous, il ne suffit pas de s'extasier sur un NOMBRE de créations d'entreprises, mais de le rapporter au reste de la population. Cette stabilité peut s'expliquer par une augmentation de la population des actifs qui absorbe la hausse des entreprises, par ex.
Une part importante de cette stabilité peut ainsi s'expliquer par le nombre de fermetures d'entreprises. Il faut mettre ces deux nombres en relation. Je n'ai à ma disposition que le nombre de défaillances (https://www.insee.fr/fr/statistiques/2015359).
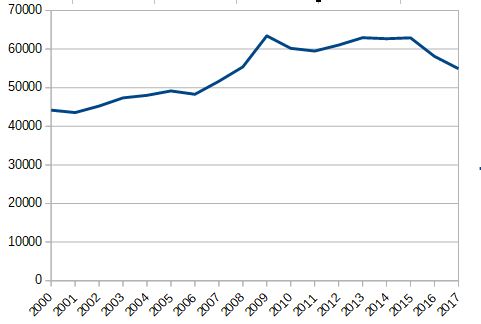
Cette baisse des défaillances en 2016-2017 n'explique pas la baisse de la part de non-salariés dans l'emploi durant la même période. Il y a donc d'autres facteurs (cumul d'emplois, fermeture non-liée à une défaillance, etc.).
Il est ainsi intéressant de constater que si le nombre d'emplois a connu une croissance nette depuis 1954, la part d'emploi non-salarié n'a fait que chuter. On est ainsi passé d'une personne sur 5 en 1970 à une personne sur 10 en 2017 (https://www.insee.fr/fr/statistiques/1406901?sommaire=1406870).

Est-ce un problème ? Pas en soi. Il faut mettre cela en relation avec un fait surprenant : 30% des salariés travaillent pour 243 entreprises. Oui, je répète, presque le tiers des salariés travaille pour moins de 0,005 % des entreprises (j'ai pas déduit les entreprises individuelles)

(source à lire : https://www.insee.fr/fr/statistiques/1379705)
Ce qui nous fait, en France, que plus du quart de l'emploi est concentré dans 0,005 % des entreprises, du coup.
D'autres chiffres sur le sujet pour vous rendre compte de la concentration : https://www.lemonde.fr/economie/article/2016/11/08/tout-ce-que-vous-avez-toujours-voulu-savoir-sur-les-entreprises-francaises-en-10-chiffres_5027592_3234.html
Il me faudrait bien plus de temps pour exposer l'ensemble de mes recherches (qui ne sont pas terminées, loin de là).
Ce qu'il faut retenir, c'est que d'une part cette augmentation de la création d'entreprises n'est pas nouvelle, mais qu'elle ne contrebalance ni le chômage ni la baisse drastique des indépendants.
Que d'autre part cette baisse des indépendants révèle une concentration extrême du salariat. Que tout cela est une tendance que l'on peut observer sur la longue durée. L'uberisation, cause de la hausse des créations d'entreprises ? C'est l'arbre qui cache la forêt.
Note
Bonjour @medialis, j'imagine que vous travaillez d'arrache-pied sur la prochaine version du site de la MDPH (vous avez sans doute constaté quelle honte c'est d'avoir un site à destination des handicapés qui n'est pas pleinement accessible).
C'est pour quand ?
Note
Message d'intérêt général. Ne dites plus « J'aime bien Platon mais je préfère Aristote ». Dites « Φίλος μεν Πλάτων, φιλoτέρα δε ἀλήθεια ». Ou en latin « Amicus Plato, sed magis amica veritas ». Perso je penche plus pour « Inimicus Plato, sed magis inimica falsitas » (Tarski)
Pierre Beyssac 🇪🇺🇺🇦 (@pbeyssac): "- la limite à 80 km/h a provoqué une forte baisse de mortalité, comme prévu - la destruction de radars en novembre/décembre a…" / Twitter
Aristotle (@AristotlesStgra): "Hi, I'm Aristotle. I'm sometimes called "The Philosopher." You may know me from most of the conceptual architecture of…" / Twitter
Servitude et soumission - Science et philosophie - Conférences en ligne - Ressources - Cité des sciences et de l'industrie
Grand Débat National : le piège - YouTube
Bonne analyse qui rejoint pas mal de mes réflexions sur le sujet (cotisations et répartition notamment)
